Optimisation is at the core of AI research. We spawn instances of massive models with trillions of parameters and then try to optimise their parameters towards some goal, typically represented by a loss function. We’ve become really good at this type of optimisation because it has a key property: we can calculate the gradient. Packages such as PyTorch automatically calculate the expected changes in our loss function if we were to tweak parameters (the gradients) which allows us to make meaningful progress towards the goal. But what if you don’t have gradients?
There’s a whole class of optimisation problems which are not gradient based, including heuristic-based methods. These methods have to deal with what little information they have, typically evaluations of the function at chosen points. An example problem I came across which warranted such a method was choosing constants for an arbitrarily defined function. Imagine the simplified case:
def add_one(x):
a = 0
x += a
return x
What should we choose for a? Obviously, it’s 1, but how could we get that result through optimisation? (In this case we could actually get away with gradient based methods with this function, but there are many cases where we cannot, e.g. argmax or any other step function.)
Nelder Mead Optimisation
A neat way to address this problem is through Nelder Mead optimisation, or the Simplex Search method. This approach relies on evaluations of the function at key points which are chosen through an adaptive method that can explore the function.
At the heart of the method is the simplex. It’s a N+1 dimensional object in a N dimensional space, for example, a triangle in a 2D space. Given this simplex, the method goes through the following steps:
- Reflect: move away from the worst point, about the other points.
- Expand: if that worked well, move away even more.
- Contraction: if that didn’t work well, stay closer.
- Shrink: if none of that worked, contract towards the best point.
These can be seen in the figure below.
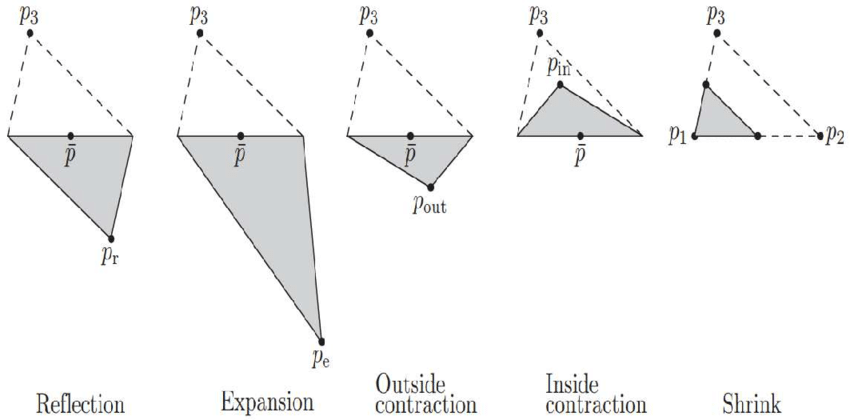
While heuristic-based methods such as Nelder Mead cannot guarantee optimal convergence, they often work in practice, making them a good choice when facing these sorts of problems.
Conclusion
Nelder Mead and other gradient-free optimisation methods remind us that not all problems are neatly differentiable. In AI and beyond, we often encounter functions that are discontinuous, noisy, or otherwise unsuited to gradient-based approaches. By iteratively exploring the function through evaluation points and adapting the search based on successes and failures, methods like Nelder Mead provide a practical way to make progress even when classical calculus tools fail.
Ultimately, the choice of optimisation method comes down to the problem at hand. When gradients are available, gradient descent and its variants are extremely powerful. When they are not, heuristic approaches offer a flexible, intuitive alternative. Understanding both paradigms equips us with a broader toolkit for tackling the diverse and often messy optimisation challenges we face in research and real-world applications.
