The Hierarchical Reasoning Model (HRM) introduces a biologically inspired recurrent architecture designed to overcome the reasoning limitations of standard Transformers and Chain-of-Thought (CoT) prompting. Comprising two interdependent modules—a slow, high-level planner and a fast, low-level executor—HRM achieves deep computational reasoning in a single forward pass without pretraining or intermediate supervision. With just 27M parameters and 1,000 training examples, it surpasses much larger models on benchmarks like ARC-AGI, Sudoku-Extreme, and Maze-Hard, demonstrating near-perfect accuracy on tasks that typically require symbolic search and backtracking.
HRM’s training pipeline leverages a one-step gradient approximation and deep supervision to avoid the memory overhead of backpropagation through time, enabling efficient convergence and scalability. Its adaptive computation mechanism dynamically allocates reasoning depth based on task complexity, and its internal state organization mirrors cortical dimensionality hierarchies observed in neuroscience.
Most interestingly, they claim their model performs better than default reasoning models on ARC-AGI tasks (both ARC-AGI-1 and ARC-AGI-2). This is not the best comparison as SoTA ARC solutions perform fine-tuning on ARC, test-time fine-tuning as well as various other techniques, but still a promising result to see. In this post, I’ll share my findings reproducing their results.
Reproducing HRM
Given they share a pre-trained model for ARC-AGI-2, it should be relatively straightforward to validate their results.
The key steps it took to get the codebase working:
- Download pre-trained model from HF: Only one for ARC-AGI-2 so easy to choose.
- Update evaluation codebase to remove distributed workflow: I’m only working on 1 GPU so it makes it unnecessarily complicated.
- Remove flash attention: flash attention is great, but it’s a little trickier to install so I changed it to the default torch scaled dot product attention. This also required some transposes to handle differences.
- Build dataset: the codebase comes with links to the ARC data, but first you must build a torch dataset to work with the model. The way it’s setup requires you to build a database with all examples and augmentations - over 1M data points. This is slow and unnecessary. I reduced to just 10 augmentations.
- Re-initialise puzzle embedding layers: the model is trained with a specific embedding for each specific input/output pair but this breaks when you change the dataset construction. I initialised this all to zero, meaning the model must predict the output based purely on the input. This is obviously problematic, as you’re asking it to solve an input without explicitly stating what the demonstrations are. As we’ll see, the model does have the information stored in its weights, but it’s not ideal.
Following all the above, it took around 30m to prepare the dataset of 16K samples, then 30m to complete the evaluation for ARC-AGI-1. ARC-AGI-2 was around the same.
Results
In short: it completely fails on ARC-AGI-2 evaluation with 0% accuracy (vs. 5% reported), but gets a 41% accuracy on ARC-AGI-1 (very close to the reported 40%). ARC-AGI-2 is harder so you’d generally expect lower performance, but this model was specifically trained to perform well on ARC-AGI-2 so I’m not sure what led to this outcome. Looking deeper at the predictions for ARC-AGI-2, the model was often understanding the task, but just failing to get the exact result. This is what makes ARC so difficult, it needs pixel-perfect accuracy.
One of the interesting things about HRM is that it directly provides uncertainty estimates, in contrast to typical LLM-based approaches which either lean on token probabilities or sampling, neither of which are robust. We can check how useful these uncertainty estimates are by measuring the correlation between accuracy and uncertainty. Specifically, we use the model’s halting logits to get a probability after applying sigmoid. This is also not a direct uncertainty in the answer, but it does indicate when the model is confident enough to stop further refinements.
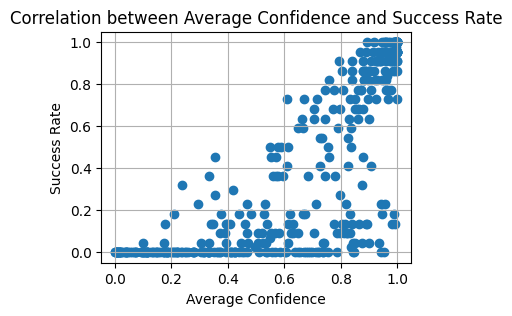
Looking at the plot, there is a clear correlation between the predicted confidence and success rate (pearson r correlation of 0.8), though they’re not calibrated well. The model is rarely conservative in its predictions, the success rate is almost always below the model’s confidence. On the other hand, the model can have confidence exceeding 95% yet be 100% wrong in its predictions.
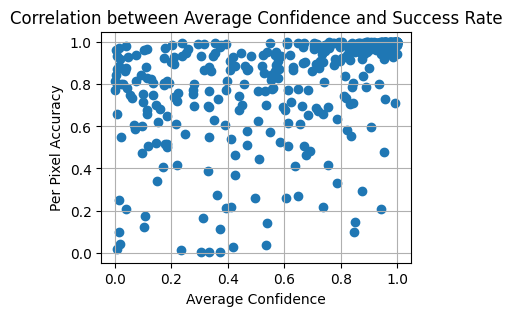
We can go a step further and check the per-pixel accuracy. Here we see that the model can still have very low per-pixel accuracies with high confidence. It also shows that even some of the low confidence predictions (<10%) can score really high per-pixel accuracies (>90%). This isn’t hugely surprising though, as in many ARC tasks by simply reproducing the input you can get fairly good results.
The authors share some interesting visualisations which show the intermediate steps during the model’s reasoning. The code to produce these figures wasn’t included and I haven’t prioritised producing them just yet, though it shouldn’t be too difficult. I’ll add it to the backlog as it may give some deeper understanding of the reasoning process of the model as it solves ARC problems.
Improvements
I don’t like that each I/O pair has a specific embedding. It makes sense that a task should have an embedding, so that information between the demonstration pairs can be shared, but that doesn’t appear to be how it’s set up. There are a few ways around this:
- Use a per-task embedding (e.g. 0934a4d8): this is reasonable and can be leveraged at test-time by extending the embedding space and fine-tuning it on the task.
- Apply meta learning techniques: learning the embeddings at test-time is a little wasteful, as there are likely things we could carry over from our pre-training. For example, based on the input it might be a puzzle that leverage symmetry. This could be combined with the learned embeddings to get a good start and a more precise result.
In the paper the authors claim that the model can perform backtracking and tree search as a way to solve puzzles. However, the only evidence presented is an example of a Sudoku puzzle in which the model iteratively improves upon its attempts, getting fewer and fewer attempts as it proceeds. This seems like very weak evidence and it would be nice to see more discussion and detail on this. For example, how are the latents that underscore the outputs shown evolving? How about within the ‘low frequency’ layers? What’s the ‘thinking’ process happening there?
Whenever I see hierarchical models like this (e.g. Hierarchical Reinforcement Learning) I can’t help but ask: why not one extra layer? The authors motivate the second layer based on slow and fast brainwave patterns, but there’s a lot more detail than this. Fast brainwaves could be split out between Gamma and Beta brainwaves, while slow brainwaves could be split to Theta, Alpha and Delta; and I’m sure there are more possibilities. I am curious what added benefit this would have and if two layers is already close to maximising the returns.
Conclusion
The Hierarchical Reasoning Model offers an intriguing step toward reasoning architectures that bridge symbolic search and neural methods, achieving strong results on complex reasoning tasks with minimal parameters and data. However, my reproduction highlights that its performance is fragile—especially on ARC-AGI-2—and its claims around backtracking, hierarchical reasoning depth, and uncertainty calibration need stronger empirical support. Future work should explore richer hierarchical structures, improved task embedding strategies, and more transparent analyses of the model’s internal reasoning dynamics. Despite its limitations, HRM opens a promising line of research for reasoning-focused AGI systems.
