We use functions every day to do useful things, but what is a function? A collection of lines of code? A graph? Let’s explore various representations that can be useful in different scenarios.
Examples
As running examples, we’ll use a few solution functions for the ARC Prize from Michael Hodel’s ARC DSL. These functions utilise various helper functions which we’ll not define and take as known (e.g. hmirror, vconcat), similarly there are various constants (e.g. THREE, TRUE). The following are three examples of increasing complexity:
def solve_4c4377d9(I):
x1 = hmirror(I)
O = vconcat(x1, I)
return O
def solve_8e1813be(I):
x1 = replace(I, FIVE, ZERO)
x2 = objects(x1, T, T, T)
x3 = first(x2)
x4 = vline(x3)
x5 = branch(x4, dmirror, identity)
x6 = x5(x1)
x7 = objects(x6, T, T, T)
x8 = order(x7, uppermost)
x9 = apply(color, x8)
x10 = dedupe(x9)
x11 = size(x10)
x12 = rbind(repeat, x11)
x13 = apply(x12, x10)
O = x5(x13)
return O
def solve_f15e1fac(I):
x1 = ofcolor(I, TWO)
x2 = portrait(x1)
x3 = branch(x2, identity, dmirror)
x4 = x3(I)
x5 = leftmost(x1)
x6 = equality(x5, ZERO)
x7 = branch(x6, identity, vmirror)
x8 = x7(x4)
x9 = ofcolor(x8, EIGHT)
x10 = uppermost(x9)
x11 = equality(x10, ZERO)
x12 = branch(x11, identity, hmirror)
x13 = x12(x8)
x14 = ofcolor(x13, EIGHT)
x15 = ofcolor(x13, TWO)
x16 = rbind(shoot, DOWN)
x17 = mapply(x16, x14)
x18 = height(x13)
x19 = apply(first, x15)
x20 = insert(ZERO, x19)
x21 = insert(x18, x19)
x22 = apply(decrement, x21)
x23 = order(x20, identity)
x24 = order(x22, identity)
x25 = size(x15)
x26 = increment(x25)
x27 = interval(ZERO, x26, ONE)
x28 = apply(tojvec, x27)
x29 = pair(x23, x24)
x30 = lbind(sfilter, x17)
x31 = compose(first, last)
x32 = chain(decrement, first, first)
x33 = fork(greater, x31, x32)
x34 = chain(increment, last, first)
x35 = fork(greater, x34, x31)
x36 = fork(both, x33, x35)
x37 = lbind(lbind, astuple)
x38 = lbind(compose, x36)
x39 = chain(x30, x38, x37)
x40 = apply(x39, x29)
x41 = papply(shift, x40, x28)
x42 = merge(x41)
x43 = fill(x13, EIGHT, x42)
x44 = chain(x3, x7, x12)
O = x44(x43)
return O
Text
The most familiar form of a function is its text form which was used to communicate the examples above. It’s human readable, can nicely handle comments and reads clearly top to bottom. While I’d argue this is the easiest to methodically analyse, it doesn’t quickly give you an idea about how data is flowing in the function or the crucial failure points, among other things.
Tokenised
The majority of the current SOTA code generators take the text form and tokenise it to feed into a transformer (though methods exist to tokenise at the character level). Since the text format is naturally a sequence, it suits the model architecture well. There are various tokenizers available, including code-specific ones. We’ll look at GPT-2’s BPE (similar to GPT-4), Code Llama (code-specialised, instruction-tuned) and another code model StarCoder (not instruction-tuned). Let’s see how they process the text differently. Below is the tokenisation for our first function (ignoring the first line):
GPT-4 (BPE): ['Ġ', 'Ġ', 'Ġ', 'Ġx', '1', 'Ġ=', 'Ġh', 'mir', 'ror', '(', 'I', ')', 'Ċ', 'Ġ', 'Ġ', 'Ġ', 'ĠO', 'Ġ=', 'Ġv', 'con', 'cat', '(', 'x', '1', ',', 'ĠI', ')', 'Ċ', 'Ġ', 'Ġ', 'Ġ', 'Ġreturn', 'ĠO']
Code LLaMA (Code-Specialized): ['▁▁▁', '▁x', '1', '▁=', '▁h', 'mir', 'ror', '(', 'I', ')', '<0x0A>', '▁▁▁', '▁O', '▁=', '▁v', 'concat', '(', 'x', '1', ',', '▁I', ')', '<0x0A>', '▁▁▁', '▁return', '▁O']
StarCoder (Code-Specialized): ['ĊĠĠĠ', 'Ġx', '1', 'Ġ=', 'Ġh', 'mirror', '(', 'I', ')', 'ĊĠĠĠ', 'ĠO', 'Ġ=', 'Ġv', 'concat', '(', 'x', '1', ',', 'ĠI', ')', 'ĊĠĠĠ', 'Ġreturn', 'ĠO']
The first observation is that the code models have a token for the concat function, as opposed to using subtokens. This is expected to be good as the models will properly learn the meaning of these functions compared to if it was split into two tokens as in BPE. Following this, StarCoder also keeps mirror as one token (though not hmirror) likely because it has more weight towards code than natural language compared to the other models. The other notable difference is that the the code models know that collections of spaces are often used at the start of the text and tokenise these as one while BPE has four separate tokens.
Tokenising the more complex functions shows similar results.
As expected, tokenising doesn’t help us understand functions a lot, it’s a mechanism for LLMs to understand and process text. If we went a step further and converted the tokens to the embeddings it would be even worse… That said, it does give us some insight into which text might be more meaningful as “concat” was given a dedicated token and “x1” was not.
ASTs
Abstract Syntax Trees are tree-based representations of functions. They conserve the syntactic and hierarchical structure of the code. The nodes represent language constructs (e.g. assign, call). They are focused on the syntax of the program and faithfully representing it in detail.
Below is an example AST for the most basic solution function:
Module(
body=[
FunctionDef(
name='solve_4c4377d9',
args=arguments(
posonlyargs=[],
args=[
arg(arg='I')],
kwonlyargs=[],
kw_defaults=[],
defaults=[]),
body=[
Assign(
targets=[
Name(id='x1', ctx=Store())],
value=Call(
func=Name(id='hmirror', ctx=Load()),
args=[
Name(id='I', ctx=Load())],
keywords=[])),
Assign(
targets=[
Name(id='O', ctx=Store())],
value=Call(
func=Name(id='vconcat', ctx=Load()),
args=[
Name(id='x1', ctx=Load()),
Name(id='I', ctx=Load())],
keywords=[])),
Return(
value=Name(id='O', ctx=Load()))],
decorator_list=[])],
type_ignores=[])
Note the detail, including all the unused values. We can also represent this text as a graph (hiding the unused lists).
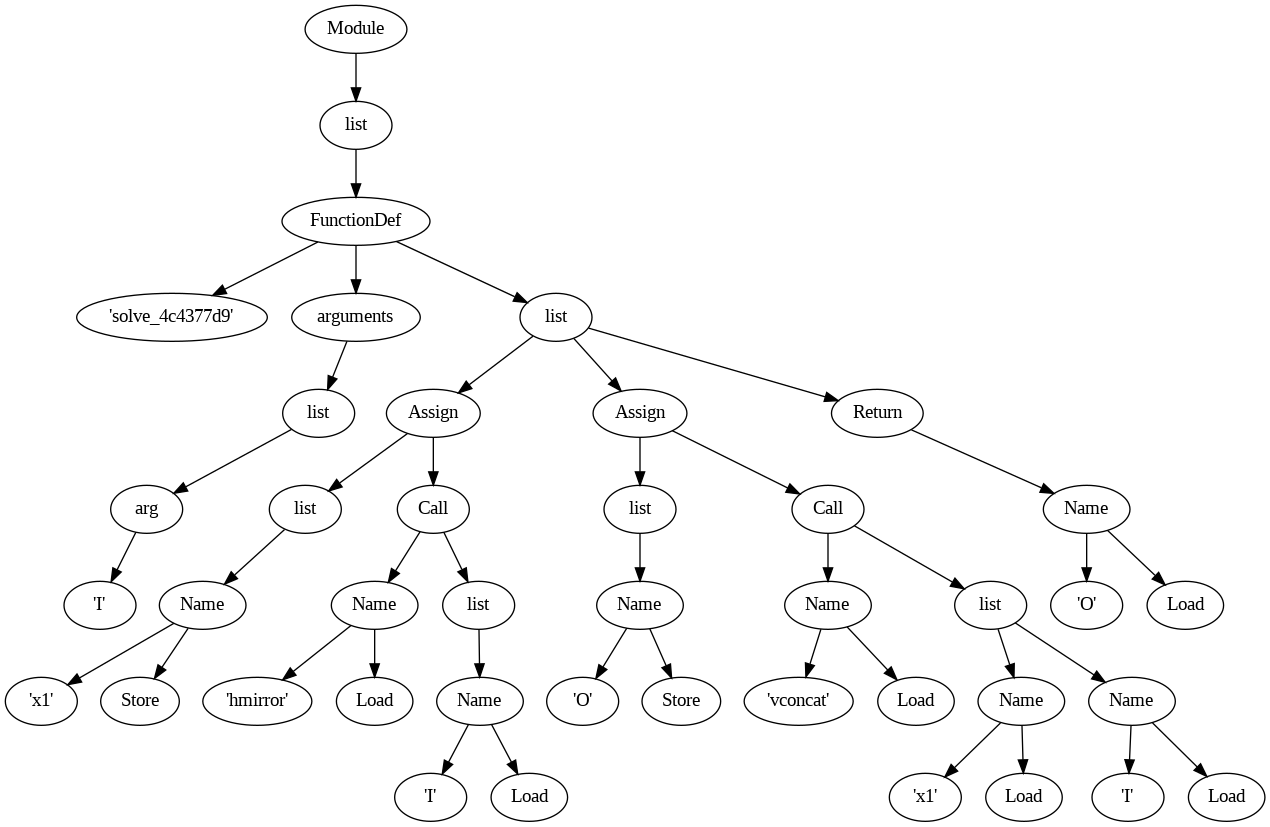
Tracing through either the text or visual representation we can reconstruct the initial Python code. Not without a bit of pain.
Computation Graphs
Computation graphs are also graph representations of functions, however they differ significantly in their mappings. In a computation graph, nodes represent computations or variables and edges represent data dependencies. They’re great for representing the flow of values during execution. They can also be much simpler to mentally process than ASTs.
Below is the representation for the simplest program.
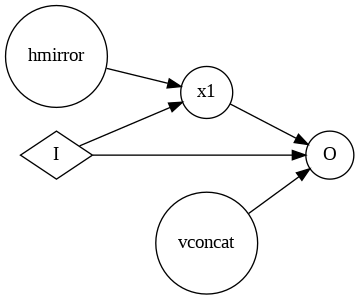
This is a whole let simpler and gets the idea across of what the function is doing. We can now try looking at one of the more complex functions.
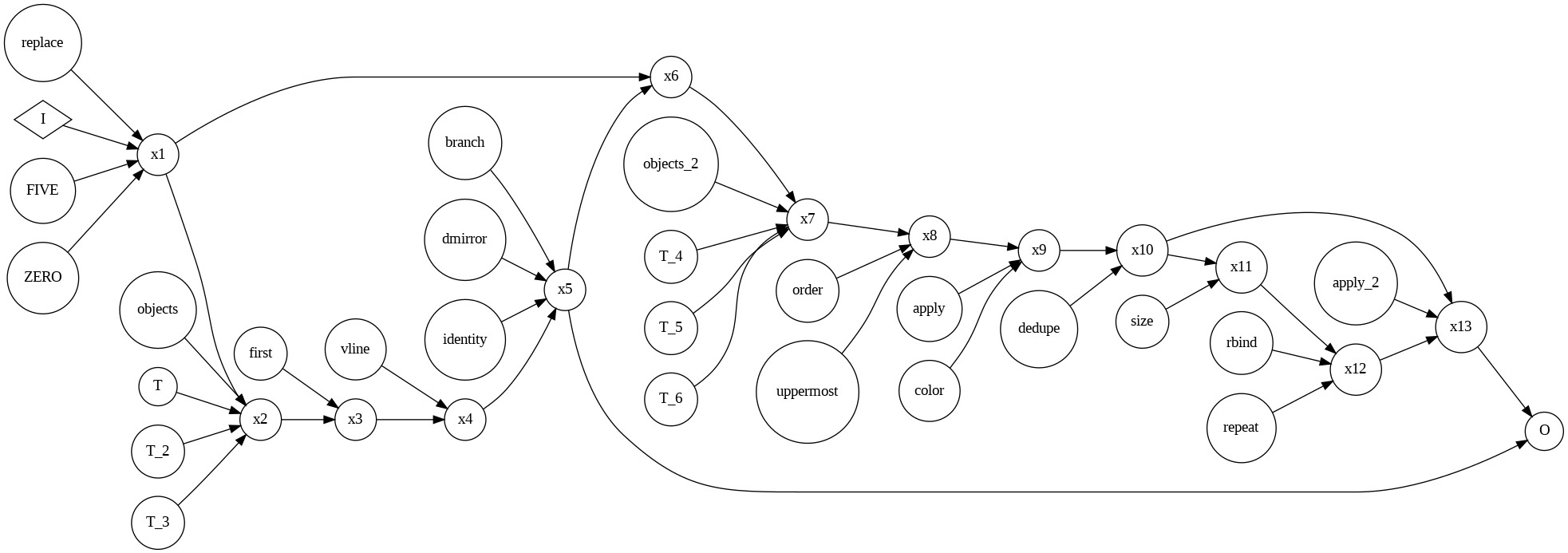
This format is great to understand the general idea of what the function is doing. Starting at the left we see the input we start with and on the right the output we aim for. We see that initially the input is modified and then that it is used in two separate calculations. This graph also helps us to see how many operations are done in series (e.g. the long stretch of x6 to x13) and what could be done in parallel (not much in this case).
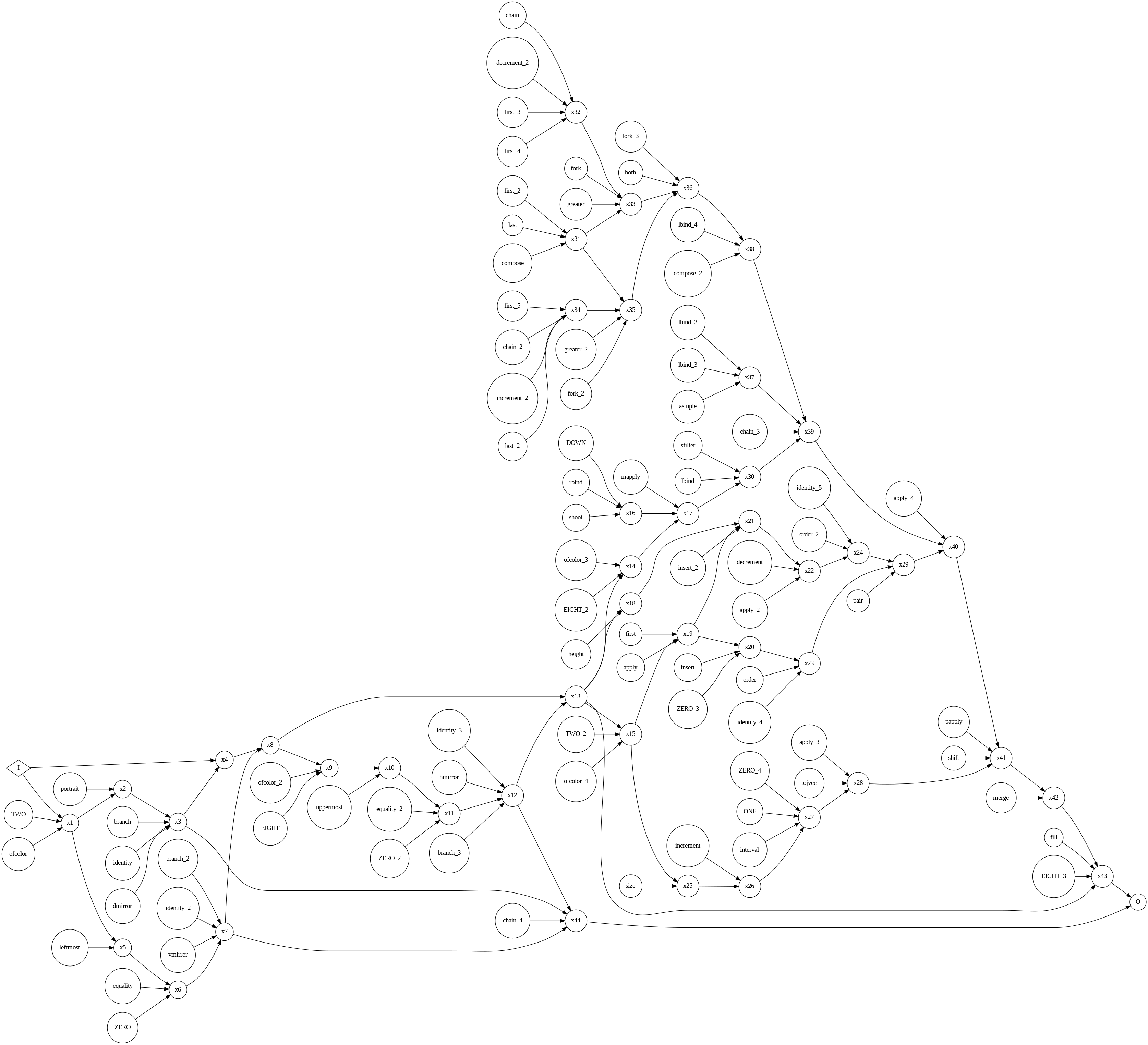
As a bonus, we can also visualise the most complex function, but it’s big. We can at least note in this example the potential for parallel computation as there are various entrypoints for the code (e.g. x31, x32, x34) which don’t depend on the initial input.
Use Cases
Each of these representations have different use cases. Functions in their standard text form are how we create and modify functions. Tokenised forms are useful for parsing text into machine-readable formats. ASTs give full descriptions of programs and are great for code analysis or program synthesis. Finally, computation graphs can give a quick overview of program structure and are useful for optimisation with machine learning applications.
Conclusion
As we’ve seen, there are many ways to represent functions and it’s great to be able to parse each type and choose which to use depending on the situation you find yourself in.
