Sometimes when reading books it can be hard to get a grasp for a problem in practice. This video popped up on IG showcasing one of the important principles of multi-agent systems.
When building multi-agent systems, it’s important to plan in negotiation methods to help them navigate situations where they’re competing for resources. This is one of the fundamental problems. That’s why it’s so amusing to see these Amazon robots fail so miserably to break out of their loop.
We can model this problem as a simple game with two agents. Each agent has two actions: 1. wait (and let the other robot pass); 2. pass the other robot. Looking at the reward table for the scenario (see below), we can see the rewards that agents get depending on their actions. It’s clear that if they were in the state where both are waiting or both are moving that the obvious action is to change your action, assuming the other agent does nothing. However, this is the problem. The other agent sees the symmetric scenario and also changes their action. This causes an oscillation between states, making it impossible for them to reach a good state. This good state is better known as a pure strategy Nash equilibrium.
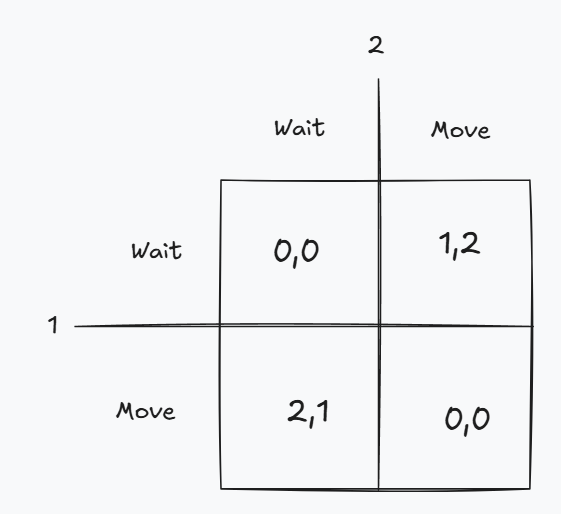
By now it should be no surprise that this is a classic game theory problem, known as “matching pennies”. There are other games such as the “prisoner’s dilemma” or “battle of the sexes” which exhibit other interesting properties.
There are many solutions to the problem we see above:
- Timing: decisions are being made roughly simultaneously here, but if the decisions can be made sequentially, then the agents would converge to one of the Nash equilibrium.
- Repetition rules: watching for repeated states as actions are made over time can allow you to introduce specific rules to avoid infinite loops.
- Mixed strategies: agents can be given probabilities of certain actions, as is common in reinforcement learning, meaning that with some probability they’re guaranteed to eventually break out of any loops.
- Communication: if agents clearly communicated their actions and were able to negotiate, that would lead to more optimal decisions being made.
I’d be surprised if there weren’t such solutions implemented, but it’s still funny to see systems slip up every now and then.
